Non-stationarity and bandit algorithms

I've been (re)reading the second edition of Rich Sutton's Introduction to Reinforcement Learning, and I've decided to do the programming exercises. (Previously, I followed Fermat's tradition of solving exercises on the margin.)

Exercise 2.5 is nice. It asks us to demonstrate the difficulties that sample-average methods have for nonstationary problems by experimentation. The intuition being that, as current distribution means deviate from their original values, the bandit algorithm takes longer to update its estimates with regards to what it considers the optimal action. Moving-average methods which give more weight to more recent returns tend to perform better.

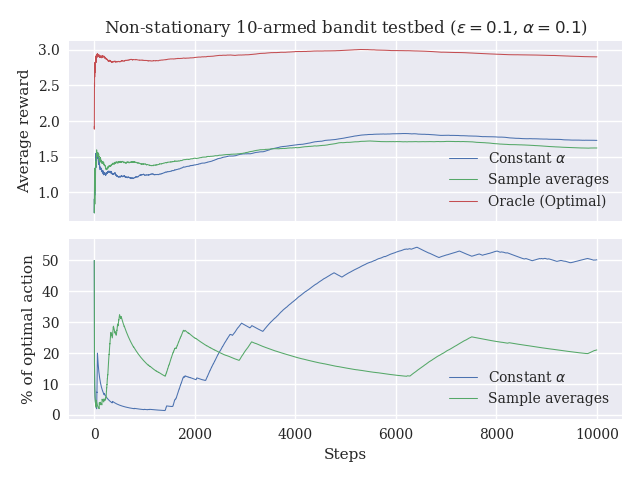
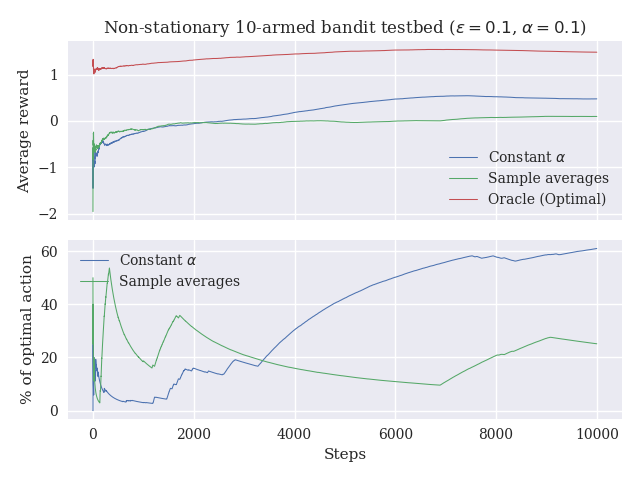
In every iteration, for each arm, we sample from a normal distribution with mean 0 and standard deviation 0.01 to change the mean reward of the arm. In practice, the reward distributions follow a random walk, and the optimal action can change at any time step.

The plots below are quite interesting. In the first one, I've plotted the rewards obtained by an oracle algorithm (the algorithm always knows which one is the optimal arm), the sample averages, and the constant step size algorithm. The exciting thing is that although the rewards are similar for both algorithms, one can see in the second plot that the weighted average (which is the same as the fixed step size) method picks the optimal action 50% of the time, while the sample averages method selects the optimal only 20% of the time.

Of course, new executions produce different results, but the general trend seems to be that, in the long run, the weighted average method performs better than the sample averages method.